Kinect: о восстановлении координат и абберациях разного рода
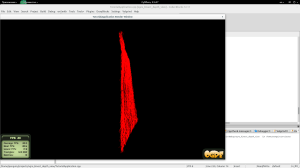
Нет. Вы не подцмайте ничего. это плоскость - вид сбоку. А точнее мой потолок. И не посмотри я на него через сенсоры кинета, то в жизни бы не узнал, насколько он “плоский”. :-D На самом деле потолок-то плоский. Но только разного рода нелинейные искажения, которые вносят сенсор и линзы не компенсируются ни встроенными калибровочными константами (которые зашиваются в каждую модель на заводе), ни функцией преобразования глубины кинекта в глубину реальную. Т.е. в метры/миллиметры.
Так что же не так?
Начнем с самого начала. Функция преобразования данных с датчика в глубину нелинейна по своей природе. Т.е. чем ближе объект наблюдения, чем с большей точностью мы можем мерять расстояние до объекта. Чем объект дальше, тем точность меньше. А это значит, что на 1 диницу шага датчика на ближнем расстоянии приходится меньше миллиметров.
На сейчас ребята из openni предлагают новую версию функции преобразования сырых данных в метрические.
0.1236 * tan(rawDisparity / 2842.5 + 1.1863)
Эта формула даст нам значения в метрах. Есть еще одна формула (она предлагалась раньше).
1/(rawDisparity * -0.0030711016 + 3.3309495161)
Теперь говорят, что она морально устарела. :)
Посмотрим на обе формулы.
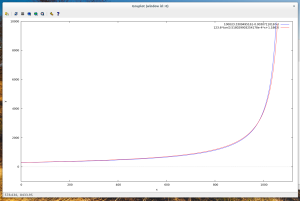
Тут мы видим, что обе дают практически одинаковый результат. Даже если их и увеличить, то расхождения будут заметны только на сильно высоких значениях датчика. Стоит заметить, что по иксу - это сырые данные. А по игреку - восстановленное расстояние (в миллиметрах. для удобства обе функции были домножены на 1000).
Ок. Расстояние есть. Дальше нужно получать как-то координаты x и y. Так как с одной глубиной ничего интересного не получиться.
Тут все интереснее.
Мы знаем из спецификации сенсора (я говорю про первую версию если что):
- угол обзора по горизонтали - 58 градусов
- угол обзора по вертикали - 45 градусов
- количество точек с датчика - 640х480
И тут у нас должно появиться подозрение на эти спеки. Почему? Потому что ничего не говорится про относительный шаг между точками по горизонтали и по вертикали.
Как мы можем предположить - расстояние измеренное от плоскости отображения до вируальной камеры должно быть всегда одинаковое, как бы мы его не мерили.
Но что же получается. А получается следующее (изображение уперто отсюда).
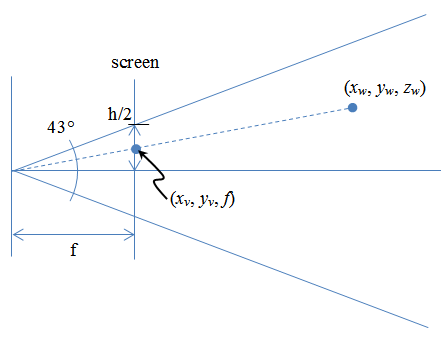
tan(45/2)/tan(58/2) = 0,747261047
А это значит, что точка по вертикали будет 0,747261047, а точка по горизонтали - 1.
Отлично. соотношение расстояний между точками по горизонтали и вертикали нашли.
Тперь надо найти точки.
После того, как данные глубины получены с кинекта формируем массив координат.
(x_v, y_v. raw_depth)
Здесь x_v и y_v - это всего лишь индексы строки и столба в двумерном массиве глубин.
x_v = [0, 639] y_v = [0, 479]
дальше надо лишь превратить эту точку в точку с реальными координатами.
z_w = 123.6 * tan(depth / 2842.5 + 1.1863)
Эм. А x_w и y_w? Тут все просто. По картинке выше мы знаем, что
x_v/f = x_w/z_w
Где f - это расстояние от камеры, то вьюпорта.
f = MAX_X/2 / tan(58/2) = 639/2 / tan(58/2) = 319.5/tan(58/2)
Или аналогично для оси ординат. Но тут не стоит забывать про коэффициент отношения между расстоянием по горизонтали и вертикали.
f = 0.747261047*239.5/tan(45/2)
Теперь все просто
x_w = (x_v - 640/2) * z_w / f y_w = (y_v - 480/2) * 0.747261047 * z_w / f
В случае с y_w не забываем про масштабный коэффициент.
Но все эти вфводы позволяют нам лиш частично восстановить изображение. И все потому, что функция глубины - это фукция от трех переменных: x_v, y_v и depth, а не просто от depth. :) Так как влияние разного рода аббераций слишком велико (не то чтобы слишком +-10 самнтиметров по краям на растоянии 2 метра).
Поэтому пока мой потолок будет зображать из себя часть поверхности сферы (или цилиндра) неопределенного радиуса.
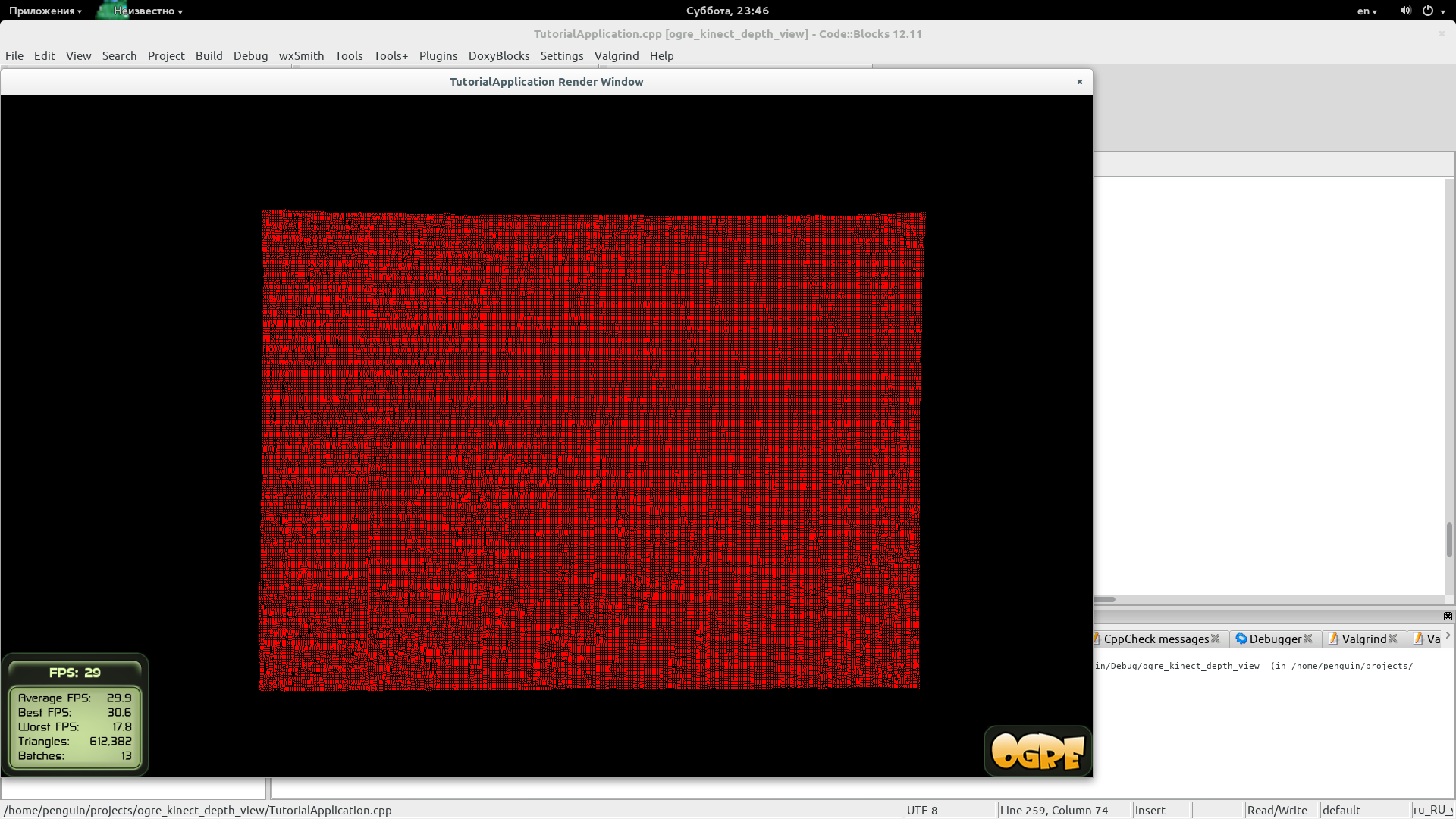
UPD